Закон Ома
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Георг Симон Ом
- Закон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
- Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
- Формула закона Ома записывается в следующем виде:
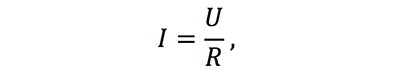
- где
- I – сила тока в проводнике, единица измерения силы тока — ампер ;
- U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт ;
- R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом .
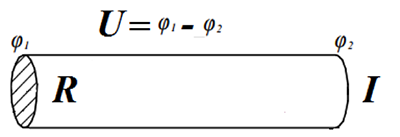
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
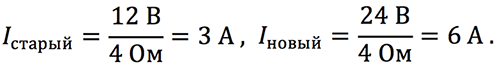
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
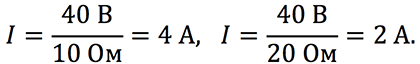
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
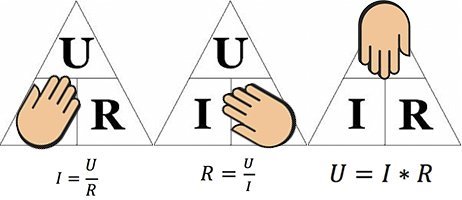
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Расчет сопротивления последовательных резисторов
Cила тока: формула
При последовательном сопротивлении нескольких резисторов соответственно увеличивается эквивалентная величина. Расчет сопротивления нескольких элементов, соединенных между собой последовательно, проводится за счет суммирования номиналов каждого элемента. Например, при соединении нескольких элементов, которые соединены в одну цепь последовательно, величина электрического сопротивления будет равной сумме уровня противодействия каждого из резисторов. Формула имеет одинаковый вид для любого количества резисторов.
Как найти сопротивление формула для последовательной цепи
Если заменить в последовательной цепи один из элементов, то соответственно изменится уровень противодействия направленному движению частиц в этой цепи. Это также повлечет изменение силы тока.
Резистор
Зависимость удельного сопротивления от температуры
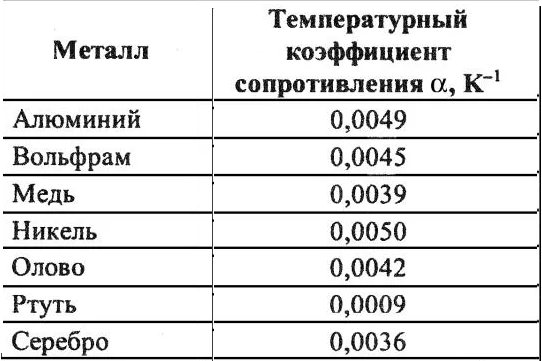
Говоря об удельном сопротивлении, нельзя упомянуть о влиянии температуры окружающей среды на его значение. Однако, это влияние будет разным для каждого материала. Это объясняется одним важным параметром $α$ — температурным коэффициентом.
Температурный коэффициент используется в формула для расчета удельного сопротивления с учетом изменения температуры:
$ρ_t =ρ_0 • $, где
- $ρ_0$ — удельное сопротивление при 20 С*,
- $α$ — температурный коэффициент,
- $t-t_0$ — разница температур.
Рассчитаем удельное сопротивление меди при -30 C и +30 C .
Пример 1
Для расчета удельного сопротивления при +30 C*, нужно взять первую формулу и подставить известные значения:
$ρ_t=ρ_0 • =0,017• =0,017•=0,0176 $
Для расчета удельного сопротивления при -30 C*, нужно взять вторую формулу и выполнить аналогичный расчет:
$ρ_t=ρ_0 • =0,017 • [1+(0,0039 • (– 30 – 20)=0,0136$
Исходя из расчетов можно сделать вполне логичный вывод, который заключается в следующем.
Замечание 2
Чем выше температура окружающей среды, тем выше удельное сопротивление.
Ток, сила тока в цепи.
Что же такое электрический ток?
Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны… Рассмотрим проводник, к которому приложено определенное напряжение:
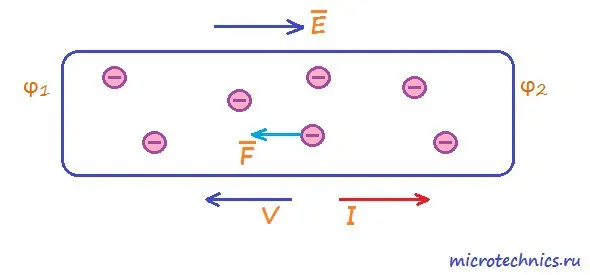
Из направления напряженности электрического поля (E) мы можем сделать вывод о том, что \phi_1 > \phi_2 (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:
F = Ee
где e − это заряд электрона.
И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток.
Ток — это упорядоченное движение заряженных частиц под воздействием электрического поля.
Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.
Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E. И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы.
Для того, чтобы оценить ток в цепи, существует такая величина как сила тока. Итак, сила тока (I) — это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер. Сила тока в проводнике равна 1 Амперу, если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон.
Мы уже рассмотрели понятия силы тока и напряжения, теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника.
Классификация резисторов
Три резистора разных номиналов для поверхностного монтажа (SMD), припаянные на печатную плату. Резисторы являются элементами электронной аппаратуры и могут применяться как дискретные компоненты или как составные части интегральных микросхем. Дискретные резисторы классифицируются по назначению, виду ВАХ, по способу защиты и по способу монтажа, характеру изменения сопротивления, технологии изготовления.
По назначению:
- резисторы общего назначения;
- резисторы специального назначения: высокоомные (сопротивления от десятка М до единиц Т, рабочие напряжения 100—400 В);
- высоковольтные (рабочие напряжения — десятки к);
- высокочастотные (имеют малые собственные индуктивности и ёмкости, рабочие частоты до сотен МГц);
- прецизионные и сверхпрецизионные (повышенная точность, допуск 0,001 — 1 %).
По характеру изменения сопротивления:
| Постоянные резисторы (для навесного монтажа). | Переменный резистор. | Подстроечные резисторы. | Прецизионный многооборотный подстроечный резистор. |
- постоянные резисторы;
- переменные регулировочные резисторы;
- переменные подстроечные резисторы.
По способу защиты:
- изолированные;
- неизолированные;
- вакуумные;
- герметизированные.
По способу монтажа:
- для печатного монтажа;
- для навесного монтажа;
- для микросхем и микромодулей.
По виду вольт-амперной характеристики:
- линейные резисторы;
- нелинейные резисторы: варисторы — сопротивление зависит от приложенного напряжения;
- терморезисторы — сопротивление зависит от температуры;
- фоторезисторы — сопротивление зависит от освещённости;
- тензорезисторы — сопротивление зависит от деформации резистора;
- магниторезисторы — сопротивление зависит от величины магнитного поля.
- мемристоры (разрабатываются) — сопротивление зависит от протекавшего через него заряда (интеграла тока за время работы).
По технологии изготовления[источник не указан 3397 дней
]:
| Проволочный резистор с отводом. | Плёночный угольный резистор (часть защитного покрытия удалена для демонстрации токопроводного слоя). |
- Проволочные резисторы. Наматываются из проволоки с высоким удельным сопротивлением на какой-либо каркас. Обычно имеют значительную паразитную индуктивность. Для снижения паразитной индуктивности почти всегда выполняются с бифилярной намоткой. Высокоомные малогабаритные проволочные резисторы иногда изготавливают из микропровода. Иные типы резисторов называются непроволочными резисторами.
- Металлоплёночные и композитные резисторы. Резистивный элемент представляет собой тонкую плёнку металлического сплава или композитного материала с высоким удельным сопротивлением, низким коэффициентом термического сопротивления, обычно нанесённую на цилиндрический керамический сердечник. Концы сердечника снабжены напрессованными металлическими колпачками с проволочными выводами для монтажа. Иногда, для повышения сопротивления, в плёнке исполняется винтовая канавка для формирования спиральной конфигурации проводящего слоя. Сейчас это наиболее распространённый тип резисторов для монтажа в отверстия печатных плат.
По такому же принципу выполнены резисторы в составе гибридной интегральной микросхемы: в виде металлических или композитных плёнок, нанесённых на обычно керамическую подложку методом напыления в вакууме или трафаретной печати.
- Металлофольговые резисторы. В качестве резистивного материала используется тонкая металлическая лента.
- Угольные резисторы. Изготавливаются в виде плёночных и объёмных. Плёнки или резистивные тела представляют собой смеси графита с органическими или неорганическими веществами.
- Интегральный резистор. Резистивный элемент — слаболегированный полупроводник, формируемый в кристалле микросхемы в виде обычно зигзагообразного канала, изолированного от других цепей микросхемы p-n переходом. Такие резисторы имеют большую нелинейность вольт-амперной характеристики. В основном используются в составе интегральных монокристаллических микросхем, где применить другие типы резисторов принципиально невозможно.
Онлайн калькулятор закона Ома: простой расчет участка цепи
Рад приветствовать тебя, дорогой читатель, в этой первой статье моего блога! Ее я посвятил самому основному закону, который должен хорошо понимать современный человек, работающий с электричеством. Мой онлайн калькулятор закона Ома создан для участка цепи. Он значительно облегчает электротехнические расчеты в домашней проводке, подходит для цепей переменного и постоянного тока.
Им просто пользоваться: прочти правила ввода данных и работай!
- Правила работы на калькуляторе
- Онлайн калькулятор закона Ома
- Простые примеры расчета Бытовая сеть переменного тока
- Цепи постоянного тока
Полезная информация для начинающего электрика
- Как использовать закон Ома на практике
Что такое участок цепи
Как использовать треугольник закона Ома
Шпаргалка электрика для новичков
Формула
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.
Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Электрический заряд. Напряженность электрического поля
Напряженность поля наряду с электрическим зарядом является фундаментальным параметром в теории электричества. При этом количественное представление о них можно получить из простых опытов, доступных школьникам.
Для простоты рассуждений будем рассматривать электростатическое поле. Это электрическое поле, которое не изменяется со временем. Такое поле может быть создано неподвижными электрическими зарядами.
Также для наших целей необходим пробный заряд. В его качестве будем использовать заряженное тело — настолько малое, что оно не способно вызывать какие-либо возмущения (перераспределение зарядов) в окружающих объектах.
Рассмотрим поочередно два взятых пробных заряда, последовательно помещенных в одну точку пространства, находящуюся под воздействием электростатического поля. Получается, что заряды будут подвергаться неизменному во времени воздействию с его стороны. Пусть F1 и F2 — это силы, воздействующие на заряды.
В результате обобщения опытных данных было установлено, что силы F1 и F2 направлены либо в одну, либо в противоположные стороны, а их отношение F1/F2 является независимым от точки пространства, куда были поочередно помещены пробные заряды. Следовательно, отношение F1/F2 является характеристикой исключительно самих зарядов, и никак не зависит от поля.
Открытие данного факта позволило охарактеризовать электризацию тел и в дальнейшем было названо электрическим зарядом. Таким образом, по определению получается q1/q2 = F1/F2, где q1 и q2 — величина зарядов, помещаемых в одну точку поля, а F1 и F2 — силы, действующие на заряды со стороны поля.
Из подобных соображений были экспериментально установлены величины зарядов различных частиц. Условно положив в соотношение один из пробных зарядов равным единице, можно вычислить величину другого заряда, измерив соотношение F1/F2.
Через известный заряд можно охарактеризовать любое электрическое поле. Таким образом, сила, действующая на единичный пробный заряд, находящийся в состоянии покоя, называется напряженностью электрического поля и обозначается E. Из определения заряда получаем, что вектор напряженности имеет следующий вид: E = F/q.
Сопротивление медного кабеля
Несмотря на то, что медь – один из лучших проводников электричества, она обладает сопротивлением. Оно незначительно – поэтому, например, при прокладке трасс небольшой длины (например, в квартире) им можно пренебречь.
Однако при прокладке трасс большой длины сопротивление медного кабеля имеет решающее значение – поскольку никому не хочется получить на «выходе» значительно меньшее напряжение, чем на «входе».
Сопротивление жилы медного кабеля
Существует три способа узнать сопротивление жилы медного кабеля – получить его из таблицы, рассчитать или же измерить специальным прибором (омметром). Первый вариант наиболее прост, но при этом не слишком точен. Таблицы, в которых указывается номинальное электросопротивление токоведущих жил медного кабеля в расчёт на 1 км длины, приведены в ГОСТ 22483-2012.
Дело в том, что табличные величины сопротивления указываются для кабелей определённого сечения и с определённым составом проводника. На практике же выясняется, что состав медного сплава может отличаться от нормативов. Особенно если речь заходит о некачественных, бюджетных кабелях.
Второй способ получения сопротивления медного кабеля – расчёт по формуле. Потребуется указать следующие значения:
- Удельное сопротивление меди ρ, которое варьируется в зависимости от процентного содержания меди в сплаве от 0,01724 до 0,018 Ом×мм²/м;
- Длину медного кабеля в метрах;
- Сечение кабеля S в мм².
Далее используется следующая формула:
Полученное сопротивление R– это сопротивление всего проводника на произвольную длину. Так что этой формулой удобно пользоваться при расчётах как длинных, так и коротких линий.
Якорь И третий вариант – это измерить сопротивление проводника самостоятельно. Он наиболее точен, поскольку показывает фактическое значение. Тем не менее, главный минус этого способа заключается в трудоёмкости.
Измерение электросопротивления токоведущих жил производится одинарным, двойным или одинарно-двойным мостом с постоянным напряжением. Конкретная методика и принципиальные схемы описываются ГОСТ 7229-76.
Сопротивление изоляции кабелей медных
Измерение сопротивления изоляции кабелей с медными токоведущими жилами является частью испытаний кабельных линий. Эти процедуры проводятся при положительной температуре окружающего воздуха.
Дело в том, что в изоляции кабеля могут находиться микрокапли влаги. При отрицательных температурах они замерзают. Кристаллы льда, в свою очередь, являются диэлектриками, то есть ток они не проводят. И, как следствие, измерения медных кабелей при отрицательной температуре не выявят наличия вкраплений влаги в изоляции.
Для измерения сопротивления изоляции используется мегаомметр. Нормативы подразумевают, что его погрешность должна составлять не более 0,2%. Так, одним из допускаемых соответствующим госреестром устройств является SonelMIC-2500 – гигаомметр, предназначенный для измерения сопротивления изоляции, степени её увлажнённости и старения.
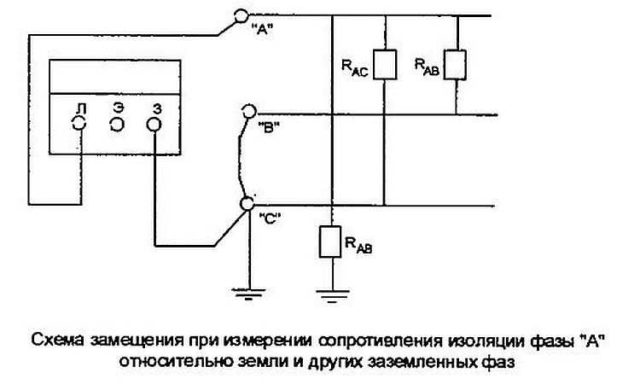
В общем виде процедура измерения сопротивления изоляции медных кабелей проводится следующим образом:
- С кабеля снимается напряжение. Его отсутствие проверяется специальным устройством;
- Устанавливается испытательное заземление на стороне, где проводится измерение;
- Жилы с другой стороны разводятся на значительное расстояние друг от друга;
- На каждую жилу подаётся напряжение. На кабели с изоляцией из бумаги, ПВХ, полимеров и резины подаётся постоянное напряжение, а на кабели с изоляцией из сшитого полиэтилена – переменное;
- В течение одной минуты замеряется сопротивление изоляции.
Измерение проходит следующим образом:
- Предположим, измеряется сопротивление изоляции жилы «А»;
- Тогда испытательное заземление подключается к жилам «В» и «С»;
- Один конец мегаомметра подключается к жиле «А», второй – к заземляющему устройству («земле»).
Стоит отметить, что конкретная методика измерения зависит от типа кабеля – низковольтный силовой, высоковольтный силовой, контрольный. Вышеприведённый алгоритм имеет общий характер.
Решение задач
Задачи, связанные с нахождением фундаментальных электрических величин, обычно простые. Но для их решения понадобится не только знать несколько формул, но и единицы измерения в СИ. В Международной системе сила тока измеряется в амперах, напряжение — вольтах, сопротивление — омах, мощность — ваттах. Нередко приходится сталкиваться с большими числами или, наоборот, маленькими, поэтому для упрощения записи используют приставки: микро, нано, кило, мега.
Вот некоторые из типовых заданий, рассчитанных на самостоятельную проработку в рамках уроков по физике для 8 класса:
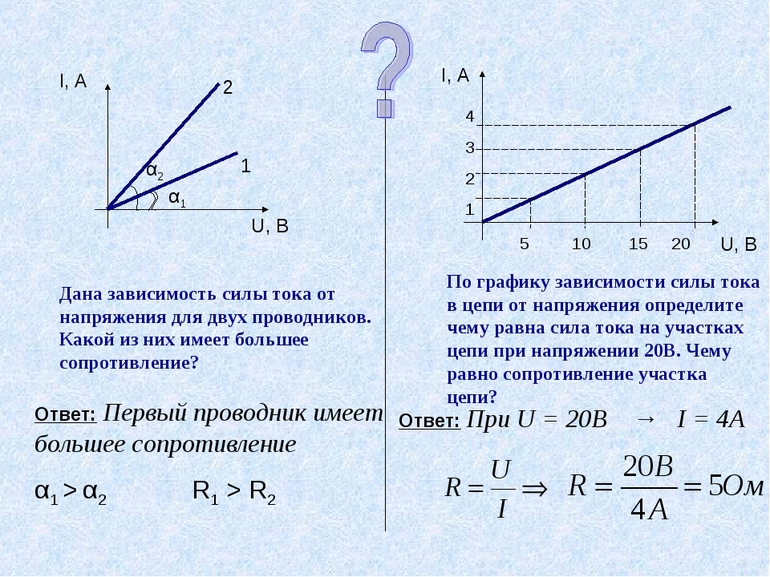
- Определить напряжение на резисторе, обладающем сопротивлением 10 Ом, если через него проходит ток силой в 1 ампер. Это простой пример, решаемый с помощью закона Ома. Согласно ему I = U/R, следовательно: U= I*R. Подставив исходные данные, можно выполнить вычисления: U= 1 A*10 Ом = 10 В.
- Найти мощность устройства, если его сопротивление равняется 1 кОм, при создаваемой разности потенциалов 10 вольт. Чтобы вычислить P, нужно определить потребление тока: I =U/R = 10/1000 = 0,01 A. Теперь воспользовавшись формулой мощности, можно найти нужный параметр: P = I*U = 0,01*10 = 0,1 Вт.
- Электрическая лампа включена в сеть с напряжением 220 В. Найти значение тока, проходящего через спираль, если сопротивление проводника равняется 30 Ом. По закону: I = U/R = 220/3 = 7,3 А.
- При напряжении 220 вольт значение тока, проходящего через дроссель, составляет 5 А. Вычислить, как изменится I, если напряжение увеличится на 20 вольт. Исходя из того, что сопротивление постоянное, можно составить пропорцию: U1 / I1 = U2/I2. Напряжение для второго случая возможно определить из выражения: U 2 = U + U 1 = 220 + 20 = 240 В. Отсюда I2 = I1 * U2 / U 1 = 5 А * 240 В / 220 В = 5,45 A.
Закон Ома для цепи переменного тока
В цепи переменного тока сопротивление кроме активной, может иметь как емкостную, так и индуктивную составляющие. Рассмотрим цепь переменного тока, состоящую из резистора сопротивлением R, конденсатора емкостью C и катушки индуктивностью L, соединенных последовательно.
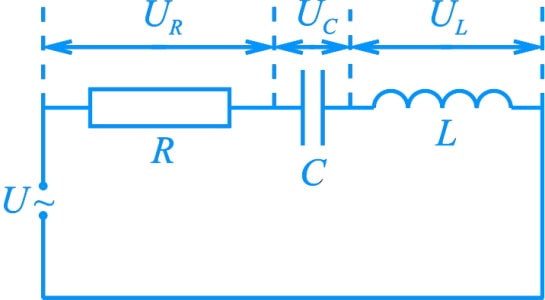
Мгновенные значения силы тока на всех элементах этой цепи одинаковы, а мгновенное значение напряжения между концами цепи равно алгебраической сумме мгновенных значений напряжений на резисторе (UR), конденсаторе (UC) и катушке индуктивности (UL).
Для того чтобы определить амплитудные (или действующие) значения напряжения и силы тока, а также сдвиг фаз между ними удобно использовать метод векторных диаграмм. Здесь действующие значения всех напряжений и токов рассматриваются как векторы, вращающиеся с угловой скоростью ω, равной циклической частоте переменного тока, а их мгновенные значения определяются проекциями этих векторов на горизонтальную ось. Так как сила тока в цепи одинакова, то построение векторной диаграммы начинается с вектора I¯0, модуль которого равен амплитудному значению силы тока в цепи. Направление этого вектора может быть любым. Зададим угол α = ωt к горизонтали.
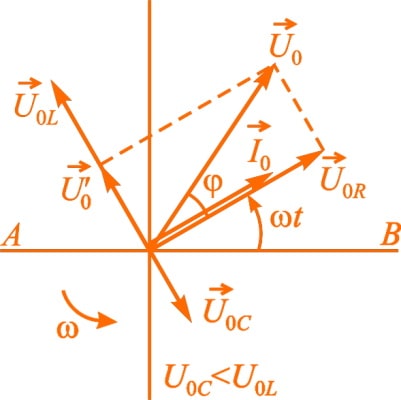
Колебания напряжения на активном сопротивлении совпадают по фазе с колебаниями силы тока, поэтому вектор U¯0R, модуль которого равен U0R = I0 × R, совпадает по направлению с вектором I¯0. Сдвиг фаз между колебаниями силы тока и колебаниями напряжения на индуктивном сопротивлении составляет π / 2, причем ток отстает по фазе от напряжения. Поэтому вектор U¯0L, модуль которого равен U0L = I0 × ωL, нужно повернуть относительно вектора I¯0 на угол π / 2 против часовой стрелки. Вектор U¯0C, модуль которого равен I0 / ωC, отстает по фазе от вектора I¯0 на π / 2, поэтому его нужно повернуть на этот угол по часовой стрелке.
Для того чтобы найти напряжение на зажимах цепи, необходимо сложить три вектора: U¯0 = U¯0R + U¯0L + U¯0C.
В первую очередь сложим векторы U¯0R и U¯0C. Модуль этой суммы U’0 = . Пусть ωL > 1 / ωC, тогда: U’0 = I0 × (ωL — 1 / ωC).
Теперь сложим векторы U¯0R и U’¯0. Модуль вектора U¯0 определяется по теореме Пифагора: U0² = U0R² + (U0L — U0C)² = I0² × R² + I0² × (ωL — 1 / ωC)². Соответственно амплитудное (действующее) значение силы тока в цепи переменного тока равно отношению амплитудного (действующего) значения напряжения на концах этой цепи к его полному сопротивлению (закон Ома для цепи переменного тока):
I0 = U0 / √(R² + (ωL — 1 / ωC)²) = U0 / Z, где:
- Z — полное сопротивление (импеданс) цепи.
- R — его активное сопротивление.
- ωL — 1 / ωC — реактивное сопротивление цепи переменного тока.
- ω = 2 × π × γ — циклическая, угловая частота. γ — частота переменного тока.
Сдвиг фаз между силой тока и напряжением равен углу φ между векторами U¯0 и I¯0. В соответствии с графиком выше ток отстает от напряжения на угол φ, причем tgφ = (ωL — 1 / ωC) / R.
Для того чтобы определить мгновенные значения напряжений на активном, емкостном и индуктивном сопротивлениях, необходимо спроектировать векторы U¯0R, U¯0L, U¯0C на прямую АВ.
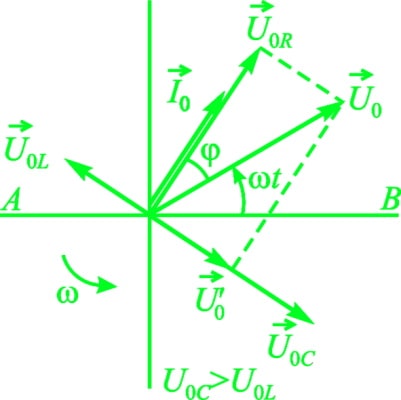
Тогда:
- UR = I0 × R × sin × (ωt + φ).
- UL = I0 × ωL × sin × (ωt + φ + π / 2).
- UC = (I0 / ωС) × sin × (ωt + φ — π / 2).
Если 1 / ωС > ωL, то:
- U’0 = I0 × (1 / ωС — ωL).
- tgφ = (1 / ωC — ωL) / R, причем ток опережает напряжение по фазе на угол φ.

































